Variaciones Simples en Lógica Matemática

Variaciones Simples en Lógica Matemática

Las variaciones simples son un concepto importante dentro del campo de la combinatoria y se utilizan cuando se desea contar las diferentes maneras de ordenar un subconjunto de elementos extraídos de un conjunto mayor. A diferencia de las combinaciones donde el orden no importa, en las variaciones simples, el orden sí tiene importancia. Este concepto es fundamental para resolver problemas que requieren la selección y organización de elementos de manera específica.

Definición y Fórmula de las Variaciones Simples

Una variación simple de un conjunto de elementos es un arreglo ordenado de elementos, en el que el orden de los elementos seleccionados sí es relevante. La fórmula general para calcular el número de variaciones simples es la siguiente:

$$ \Large V(n, k) = \frac{n!}{(n-k)!} $$

Donde:

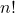• es el f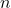actorial de .
• es el factorial de .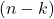

Esta fórmula cuenta el número de maneras en que podemos organizar elementos tomados de un conjunto de elementos, respetando el orden de los mismos.

Propiedades de las Variaciones Simples

Las variaciones simples tienen propiedades que son esenciales para la resolución de problemas combinatorios y de organización. Algunas de las propiedades clave incluyen:

1. Orden Importante: A diferencia de las combinaciones, en las variaciones simples el orden de los elementos seleccionados sí importa. Por ejemplo, al seleccionar dos elementos de un conjunto de tres, las variaciones posibles de son .
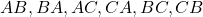2. Relación con las Permutaciones: Las variaciones simples son similares a las permutaciones en que ambas consideran el orden de los elementos. Sin embargo, mientras que las permutaciones se refieren al arreglo de todos los elementos del conjunto, las variaciones simples se limitan a arreglos de un número 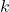de elementos.
3. Fórmula con Factorial: La fórmula de las variaciones simples muestra cómo se debe calcular el número de posibles arreglos. Al ser un subconjunto de 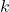elementos de un conjunto de 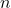elementos, debemos dividir el número total de permutaciones por las que no corresponden a las variaciones que estamos contando.

Ejemplos de Variaciones Simples

1. Ejemplo 1: Si tenemos un conjunto de 4 elementos 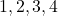y queremos seleccionar 2 elementos, el número de variaciones posibles es:

$$ \Large V(4, 2) = \frac{4!}{(4-2)!} = \frac{4 \times 3 \times 2 \times 1}{2 \times 1} = 12 $$

Las variaciones posibles son: arreglos diferentes, que incluyen: .

Ejemplo 2: Si tenemos un conjunto de 5 cartas en una baraja y queremos elegir 3 cartas con orden, el número de variaciones posibles es:

$$ \Large V(5, 3) = \frac{5!}{(5-3)!} = \frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1} = 60 $$

Las variaciones pueden ser: .

Ejemplo 3: Si tenemos un conjunto de 6 estudiantes y seleccionamos 4 para un proyecto, el número de variaciones posibles es:

$$ \Large V(6, 4) = \frac{6!}{(6-4)!} = \frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1} = 360 $$

Aplicaciones de las Variaciones Simples

Las variaciones simples tienen diversas aplicaciones en varias ramas de las matemáticas y las ciencias. Algunos de los campos donde las variaciones simples son útiles incluyen:

1. Teoría de Probabilidades: En la teoría de probabilidades, las variaciones simples se utilizan cuando se debe calcular la probabilidad de eventos donde el orden es importante, como en la selección y ordenación de objetos o elementos en experimentos aleatorios.
2. Problemas de Organización: Las variaciones simples se aplican en situaciones donde se necesita organizar elementos de un conjunto. Esto puede ser útil en la programación de actividades, la asignación de recursos o la organización de eventos.
3. Códigos y Criptografía: Las variaciones simples son útiles en problemas de codificación y criptografía, donde el orden de los elementos seleccionados (como caracteres o símbolos) juega un papel crucial en la seguridad o el análisis de los sistemas.
4. Teoría de Grafos: En la teoría de grafos, las variaciones simples se emplean para contar diferentes formas de conectar vértices en un grafo, considerando que el orden de conexión tiene implicaciones importantes.

Relación con las Combinaciones

Es importante notar que las variaciones simples se diferencian de las combinaciones en que en las combinaciones no se tiene en cuenta el orden de los elementos seleccionados, mientras que en las variaciones sí. Por ejemplo, al elegir 2 elementos de un conjunto de 3, las combinaciones posibles son , pero las variaciones posibles, considerando el orden, serían .

Conclusión

Las variaciones simples son fundamentales en la combinatoria y desempeñan un papel crucial en la resolución de problemas matemáticos relacionados con el orden de los elementos en un conjunto. Son utilizadas en diversas aplicaciones, desde la teoría de probabilidad hasta la programación de actividades y la teoría de grafos. Comprender cómo calcular y aplicar las variaciones simples es esencial para abordar muchos problemas combinatorios en lógica matemática.