Variaciones con Repetición en Lógica Matemática

Las variaciones con repetición son un concepto esencial dentro de la combinatoria y la enumeración en el ámbito de la lógica matemática. Este tipo de variaciones se utilizan cuando deseamos seleccionar y organizar elementos de un conjunto, permitiendo repeticiones y donde el orden de los elementos es importante. Es decir, a diferencia de las combinaciones, las variaciones tienen en cuenta el orden, lo que las hace útiles en muchos tipos de problemas donde la disposición específica de los elementos seleccionados juega un papel importante.

Definición de Variaciones con Repetición

Las variaciones con repetición son arreglos de elementos tomados de un conjunto, donde el orden importa y se permite la repetición de elementos. En este tipo de variaciones, cada uno de los lugares de la disposición puede estar ocupado por uno de los elementos disponibles, y es posible que varios lugares tengan el mismo elemento.

La fórmula general para calcular el número de variaciones con repetición es:

$$ \Large V(n, k) = n^k $$

Donde:

• \( n \) es el número de elementos disponibles en el conjunto.
• \( k \) es el número de lugares o posiciones a llenar con los elementos seleccionados.

Esta fórmula refleja que, para cada uno de los \( k \) lugares en la variación, tenemos \(n \) opciones posibles de selección, ya que los elementos se pueden repetir.

Propiedades de las Variaciones con Repetición

Las variaciones con repetición presentan varias propiedades que las hacen útiles en problemas combinatorios. Algunas de las propiedades clave incluyen:

1. El orden es importante: Al igual que las permutaciones, en las variaciones el orden de los elementos seleccionados sí importa. Por ejemplo, la secuencia 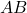es diferente de 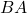, aunque ambas estén formadas por los mismos elementos.
2. Permiten repeticiones: A diferencia de las variaciones sin repetición, las variaciones con repetición permiten que los elementos se repitan en la selección. Esto es útil en situaciones donde se necesitan contar las maneras de organizar elementos con repeticiones permitidas.
3. Aplicaciones en asignaciones y secuencias: Las variaciones con repetición son esenciales para resolver problemas relacionados con la asignación de recursos o la formación de secuencias en las que el orden de aparición de los elementos es importante.

Ejemplos de Variaciones con Repetición

1. Ejemplo 1: Si tenemos 3 colores \( {A, B, C} \) y deseamos formar una secuencia de 2 colores (permitiendo repeticiones), el número de variaciones con repetición es:

$$ \Large V(3, 2) = 3^2 = 9 $$

Las variaciones posibles son: \( AA, AB, AC, BA, BB, BC, CA, CB, CC \).

Ejemplo 2: Si tenemos 4 tipos de frutas \( {manzana, banana, pera, uva} \) y queremos seleccionar 3 frutas (permitiendo repeticiones y considerando el orden), el número de variaciones con repetición es:

$$ \Large V(4, 3) = 4^3 = 64 $$

Las variaciones posibles incluyen secuencias como: \( manzana, manzana, pera; banana, pera, pera; pera, uva, uva; \dots \).

Ejemplo 3: Si se tienen 2 números \( {1, 2} \) y queremos formar una secuencia de 4 números (permitiendo repeticiones), el número de variaciones con repetición es:

$$ \Large V(2, 4) = 2^4 = 16 $$

Las variaciones posibles son: \( 1111, 1112, 1121, 1122, \dots \).

Aplicaciones de las Variaciones con Repetición

Las variaciones con repetición tienen una amplia gama de aplicaciones prácticas, especialmente en situaciones donde el orden es importante y los elementos pueden repetirse. Algunas de las principales aplicaciones son:

1. Asignación de Recursos: En problemas donde se deben asignar recursos entre diferentes grupos o personas, las variaciones con repetición se utilizan para contar las diferentes maneras en que los recursos pueden ser distribuidos, considerando que algunos recursos pueden repetirse.
2. Problemas de Secuencias: Las variaciones con repetición son útiles para contar el número de formas en que se pueden organizar secuencias de elementos, como la creación de contraseñas, la generación de combinaciones de dígitos o la disposición de elementos en sistemas de clasificación.
3. Teoría de la Información: En la teoría de la información, las variaciones con repetición son útiles para calcular el número de secuencias posibles que se pueden formar con un conjunto de símbolos, considerando que los símbolos pueden repetirse.
4. Algoritmos de Optimización: En algunos algoritmos de optimización, las variaciones con repetición se utilizan para calcular las diferentes formas en que se pueden organizar o distribuir los elementos de manera eficiente en un sistema.
5. Juegos de Azar y Simulaciones: En juegos de azar como la lotería o en la simulación de procesos aleatorios, las variaciones con repetición permiten calcular las diferentes formas de obtener un resultado dado un conjunto de elementos posibles.

Conclusión

Las variaciones con repetición son un concepto fundamental en la combinatoria y en la enumeración dentro de la lógica matemática. Este concepto es crucial para resolver problemas combinatorios en los que el orden de los elementos seleccionados es importante y donde se permite que los elementos se repitan. Las aplicaciones de las variaciones con repetición son numerosas y abarcan áreas como la teoría de la información, la asignación de recursos, y la simulación de procesos.