El triángulo es una de las figuras geométricas fundamentales en matemáticas y es la base del estudio de la trigonometría y la geometría analítica. Un triángulo es un polígono de tres lados y tres ángulos, con propiedades esenciales que se utilizan en múltiples ramas de las matemáticas.
1. Definición y Elementos de un Triángulo
Un triángulo se define como un polígono con tres lados, tres vértices y tres ángulos internos. Se denota con los vértices \(A, B, C\), y sus lados opuestos son \(a, b, c\).
Los elementos principales de un triángulo incluyen:
- Lados: Segmentos que forman el triángulo.
- Ángulos internos: Los ángulos dentro del triángulo.
- Altura: Segmento perpendicular desde un vértice hasta el lado opuesto.
- Mediatriz: Recta perpendicular a un lado que pasa por su punto medio.
- Bisectriz: Segmento que divide un ángulo en dos partes iguales.
- Mediana: Segmento que une un vértice con el punto medio del lado opuesto.
2. Clasificación de los Triángulos
Según sus Lados
- Equilátero: Sus tres lados son iguales (\(a = b = c\)).
- Isósceles: Tiene dos lados iguales (\(a = b \neq c\)).
- Escaleno: Sus tres lados son diferentes (\(a \neq b \neq c\)).
Según sus Ángulos
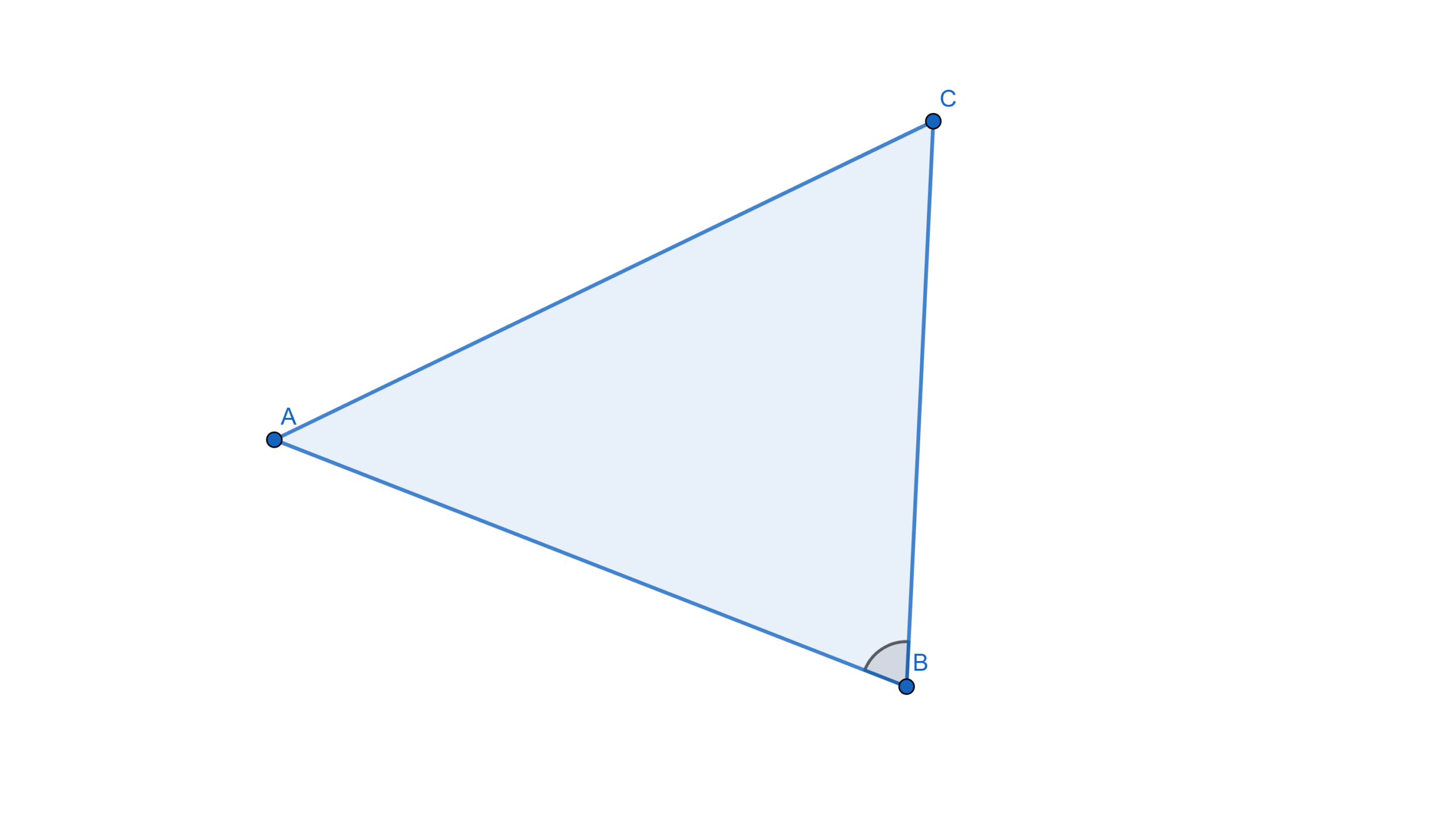 Acutángulo: Sus tres ángulos son menores a \(90^\circ\).
Acutángulo: Sus tres ángulos son menores a \(90^\circ\).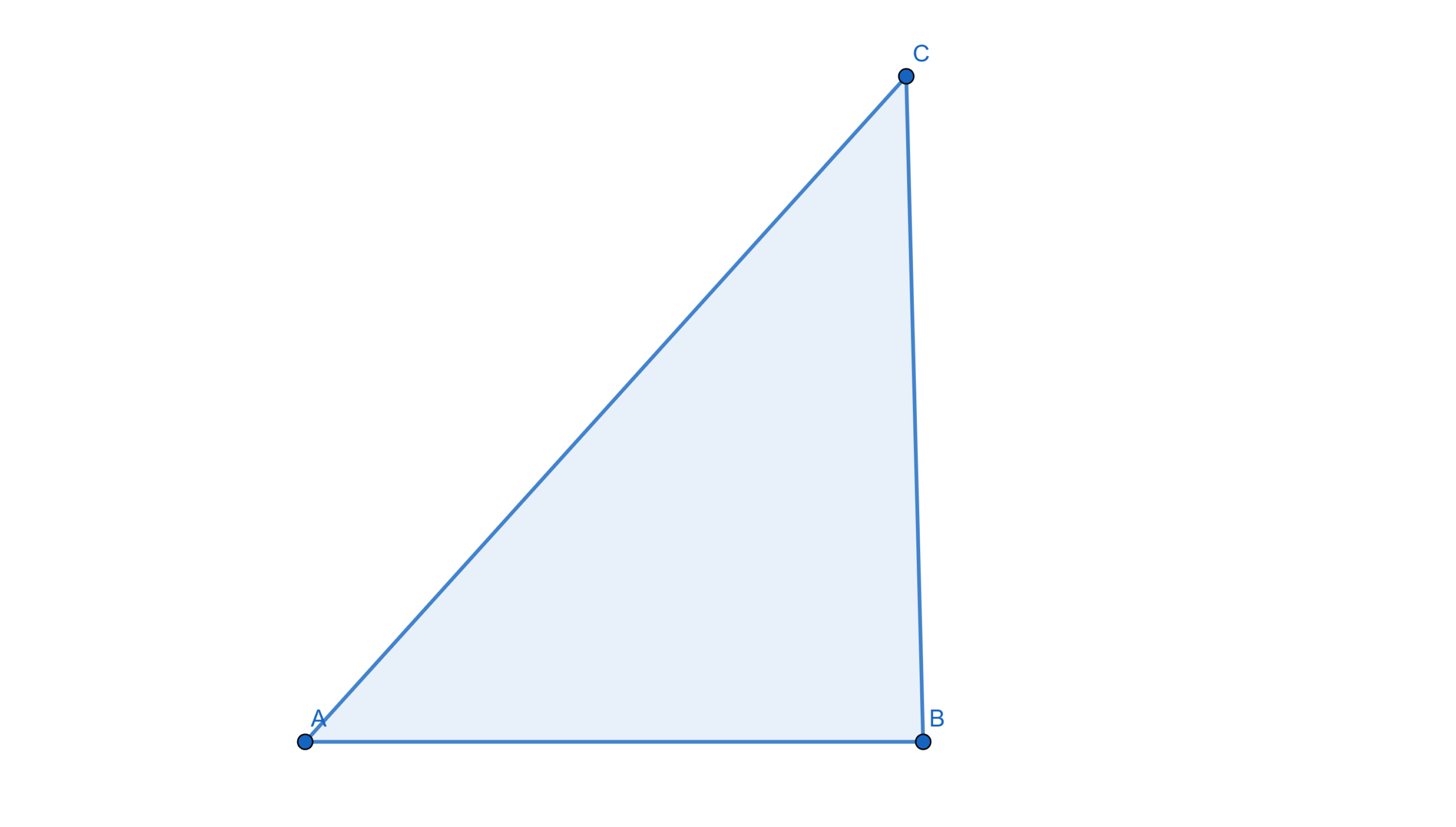 Rectángulo: Tiene un ángulo de \(90^\circ\).
Rectángulo: Tiene un ángulo de \(90^\circ\).
- Se cumple el Teorema de Pitágoras: \(a^2 + b^2 = c^2\)
- Sus lados reciben nombres específicos:
- Hipotenusa (\(c\)): el lado opuesto al ángulo recto.
- Catetos (\(a, b\)): los otros dos lados.
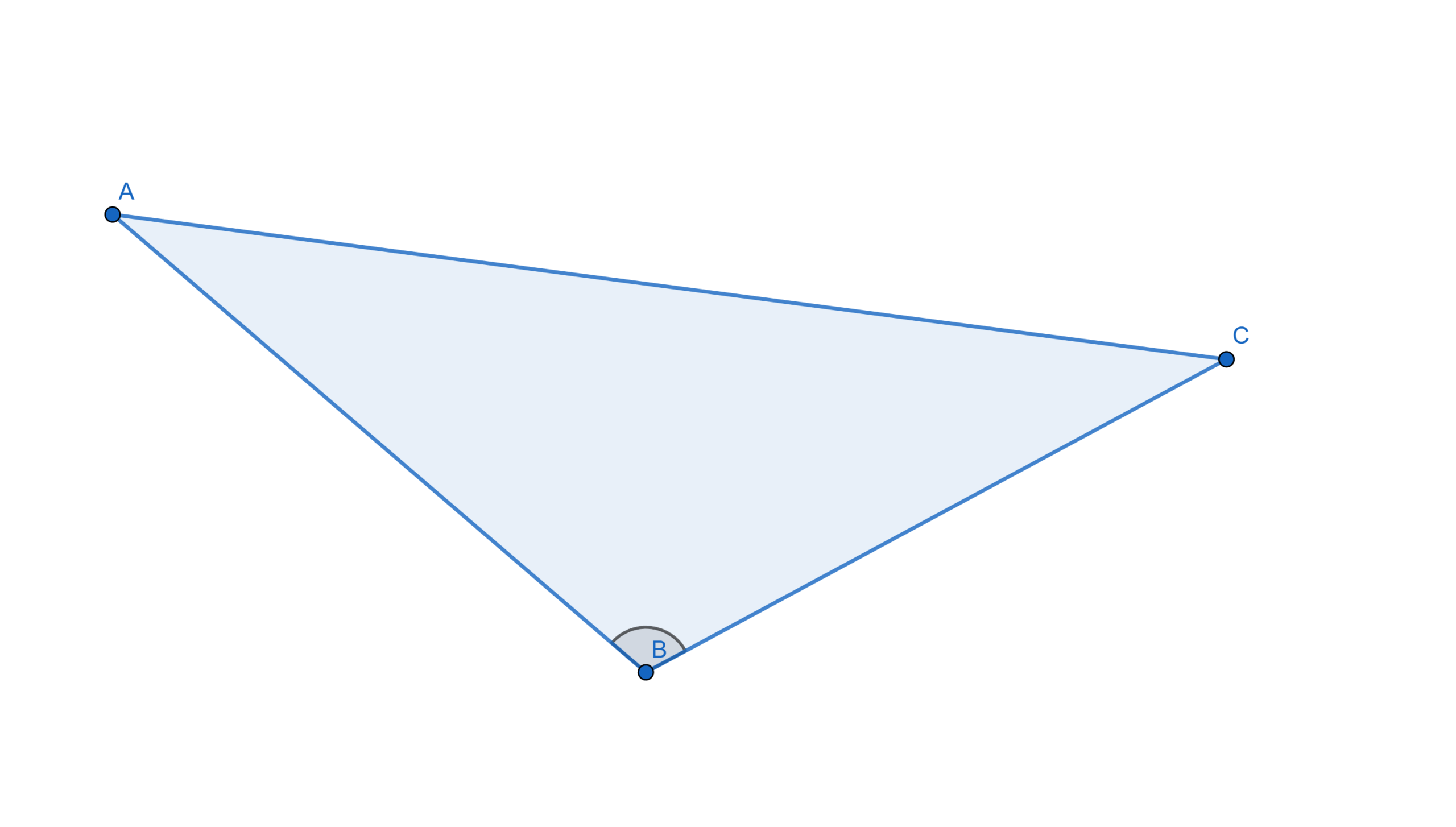 Obtusángulo: Tiene un ángulo mayor de \(90^\circ\).
Obtusángulo: Tiene un ángulo mayor de \(90^\circ\).
3. Propiedades Fundamentales de los Triángulos
Suma de los Ángulos Internos
En cualquier triángulo, la suma de los ángulos internos es siempre: $$ \Large \alpha + \beta + \gamma = 180^\circ $$
Desigualdad Triangular
La suma de dos lados de un triángulo siempre es mayor que el tercer lado: $$ \Large a + b > c, \quad a + c > b, \quad b + c > a $$
Área de un Triángulo
El área de un triángulo se puede calcular con la base (\(b\)) y la altura (\(h\)): $$ \Large A = \frac{1}{2} b h $$
Otra forma de calcular el área, si se conocen los tres lados, es con la fórmula de Herón: $$ \Large A = \sqrt{s (s-a)(s-b)(s-c)} $$
donde \(s\) es el semiperímetro: $$ \Large s = \frac{a+b+c}{2} $$
Razones Trigonométricas en un Triángulo Rectángulo
Si \(\theta\) es un ángulo en un triángulo rectángulo, se definen las siguientes razones trigonométricas: $$ \Large \sin \theta = \frac{\text{cateto opuesto}}{\text{hipotenusa}} $$ $$ \Large \cos \theta = \frac{\text{cateto adyacente}}{\text{hipotenusa}} $$ $$ \Large \tan \theta = \frac{\text{cateto opuesto}}{\text{cateto adyacente}} $$
Puntos Notables de un Triángulo
- Circuncentro (O): Es el punto de intersección de las mediatrices de los lados del triángulo. Es el centro de la circunferencia circunscrita al triángulo y equidista de sus tres vértices.
- Incentro (I): Es el punto de intersección de las bisectrices de los ángulos internos del triángulo. Es el centro de la circunferencia inscrita y equidista de los tres lados del triángulo.
- Ortocentro (H): Es el punto de intersección de las alturas del triángulo. Su posición varía según el tipo de triángulo: dentro en acutángulos, en el vértice del ángulo recto en rectángulos y fuera en obtusángulos.
- Baricentro (G): Es el punto de intersección de las medianas del triángulo. Actúa como el centro de gravedad y divide cada mediana en una proporción de 2:1.
La Recta de Euler
En cualquier triángulo no equilátero, el ortocentro (H), el baricentro (G) y el circuncentro (O) están alineados en una misma recta llamada recta de Euler, nombrada así en honor al matemático suizo Leonhard Euler. Además, la distancia del ortocentro al baricentro es el doble que la del baricentro al circuncentro.
Conclusión
El estudio de los triángulos es fundamental en geometría, trigonometría y cálculo. Comprender sus propiedades permite resolver problemas matemáticos y aplicarlos en áreas como la física, la arquitectura y la ingeniería.