Radicación

Radicación en Operaciones Fundamentales de la Aritmética

La radicación es una de las operaciones fundamentales de la aritmética y se considera la operación inversa de la potenciación. Se utiliza para determinar qué número, elevado a un exponente dado, produce un valor específico.

Definición de Radicación

La radicación se representa de la siguiente forma:

$$ \huge \sqrt[n]{a} = b $$

donde:

• \( a \) es el radicando, el número dentro de la raíz.
• \( n \) es el índice, que indica el grado de la raíz.
• \( b \) es la raíz, el número que, elevado a \( n \), da como resultado el radicando.

Por ejemplo:

$$ \large \sqrt[3]{27} = 3 \text{ porque } 3^3 = 27 $$

Propiedades de la Radicación

1. Radicación de una potencia

$$ \large \sqrt[n]{a^m} = a^{\frac{m}{n}} $$

Raíz de un producto

$$ \large \sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b} $$

Raíz de un cociente

$$ \large \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} $$

Raíz de una raíz

$$ \large \sqrt[m]{\sqrt[n]{a}} = \sqrt[m \cdot n]{a} $$

Raíz de 1

$$ \large \sqrt[n]{1} = 1 \text{, para cualquier } n $$

Casos Especiales

• Raíz cuadrada: Cuando , se omite el índice. porque .
• Raíz cúbica: Se usa cuando . porque .
• Raíz de un número negativo: Si 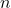es par, no existe una raíz real. Ejemplo: no tiene solución real, pero porque .

Ejemplos Aplicados

1. 
2. 
3. 
4. 
5. 

Conclusión

La radicación es una operación clave en aritmética, utilizada para deshacer potenciaciones y simplificar cálculos en múltiples contextos matemáticos. Su correcta comprensión facilita el estudio de álgebra y otros campos avanzados de las matemáticas.