Principio de la Multiplicación en Lógica Matemática
El principio de la multiplicación, también conocido como regla del producto, es un principio fundamental que se emplea en matemáticas, especialmente en áreas como la combinatoria, la probabilidad, y la teoría de conjuntos. Este principio se utiliza para calcular el número total de maneras en las que se pueden realizar dos o más eventos, actividades o elecciones que son independientes entre sí. Es una herramienta crucial en la resolución de problemas que involucran la combinación o permutación de eventos o elementos.
Definición y Enunciado del Principio de la Multiplicación
El principio de la multiplicación establece que si un evento puede ocurrir de 
maneras y otro evento independiente puede ocurrir de 
maneras, entonces el número total de maneras en que ambos eventos pueden ocurrir es simplemente el producto de y . Formalmente, si tenemos dos eventos independientes 
y 
, el número total de formas en que ambos pueden ocurrir es:
$$ \Large \text{Total de maneras} = m \times n $$
Esto se puede extender a más de dos eventos. Si tenemos 
eventos independientes, donde el primer evento ocurre de 
maneras, el segundo de 
maneras, y así sucesivamente, entonces el número total de maneras en que todos los eventos pueden ocurrir es:
$$ \Large m_1 \times m_2 \times \dots \times m_k $$
Aplicaciones del Principio de la Multiplicación
El principio de la multiplicación tiene aplicaciones en una variedad de contextos en lógica matemática, combinatoria y teoría de probabilidades. Algunas de sus aplicaciones incluyen:
- Combinatoria: El principio de la multiplicación se utiliza en combinatoria para contar el número de combinaciones posibles de elementos cuando los elementos se eligen de diferentes conjuntos. Por ejemplo, si tenemos 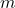opciones para elegir una prenda de ropa y 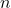opciones para elegir un accesorio, el número total de formas de combinar una prenda y un accesorio es simplemente
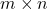. - Permutaciones y Combinaciones: En el caso de las permutaciones (cuando el orden importa) y las combinaciones (cuando el orden no importa), el principio de la multiplicación es esencial. En permutaciones, si tenemos 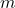elementos disponibles para el primer lugar,
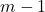para el segundo, y así sucesivamente, el número total de permutaciones es el producto de estos valores. - Teoría de Probabilidades: En la teoría de probabilidades, el principio de la multiplicación se aplica al calcular la probabilidad de que ocurran dos o más eventos independientes. Si los eventos 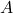y 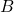tienen probabilidades
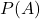y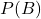 
, la probabilidad de que ambos eventos ocurran juntos es el producto de sus probabilidades:
$$ \Large P(A \cap B) = P(A) \times P(B) $$
- Teoría de Conjuntos: En la teoría de conjuntos, el principio de la multiplicación se aplica al contar el número de elementos en el producto cartesiano de dos o más conjuntos. Si el conjunto 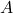tiene 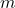elementos y el conjunto 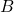tiene 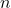elementos, el número de elementos en el producto cartesiano
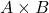es simplemente .
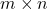Ejemplo de Aplicación
Supongamos que tenemos una tienda que vende camisetas en 
colores y pantalones en 
tamaños. Si queremos saber cuántas combinaciones diferentes de camisetas y pantalones podemos comprar, aplicamos el principio de la multiplicación, ya que estamos eligiendo una camiseta y un pantalón de conjuntos independientes. El número total de combinaciones posibles es:
$$ \Large 4 \times 3 = 12 $$
Relación con el Principio de la Suma
El principio de la multiplicación está estrechamente relacionado con el principio de la suma. Mientras que el principio de la multiplicación se aplica cuando se combinan opciones independientes (es decir, uno no afecta al otro), el principio de la suma se utiliza cuando se tienen opciones mutuamente excluyentes (es decir, una opción no puede ocurrir si la otra ya ha ocurrido). En términos sencillos, el principio de la multiplicación se usa cuando los eventos o elecciones no se excluyen mutuamente, mientras que el principio de la suma se utiliza cuando las opciones son excluyentes entre sí.
Ejemplo: Eventos Independientes
Consideremos un dado y una moneda. El dado tiene 
caras y la moneda tiene 
caras. Si tiramos el dado y la moneda, el número total de resultados posibles es el producto de las opciones disponibles para cada uno de los eventos (el dado y la moneda):
$$ \Large 6 \times 2 = 12 $$
Esto significa que hay 12 resultados posibles en total, considerando las diferentes combinaciones de resultados entre el dado y la moneda.
Conclusión
El principio de la multiplicación es una herramienta esencial en lógica matemática, combinatoria y probabilidad. Nos permite calcular el número de maneras en las que se pueden realizar dos o más eventos independientes y es fundamental para resolver problemas de conteo y probabilidad en diversas áreas de las matemáticas. Este principio es clave para comprender la estructura y las combinaciones posibles en situaciones de elección y selección, lo que lo convierte en una parte vital del análisis matemático.