La Geometría Euclidiana es una rama fundamental de la geometría, y sus principios básicos se basan en un conjunto de postulados formulados por el matemático griego Euclides en su obra Elementos. Estos postulados son las reglas fundamentales sobre las cuales se construye la geometría plana que estudiamos hoy en día.
A continuación, exploramos los Postulados de Euclides y su relevancia en el estudio de la geometría.
1. Los Postulados de Euclides
Euclides en su Elementos formuló cinco postulados que son los cimientos de la geometría euclidiana. A continuación se presentan de manera resumida:
Primer Postulado
Por cualquier par de puntos, existe una única línea recta que pasa por ellos.
Este postulado establece que entre dos puntos cualesquiera, se puede trazar una única línea recta que los conecte.
Segundo Postulado
Cualquier segmento de línea recta puede extenderse indefinidamente en ambas direcciones.
Este postulado implica que una línea recta no tiene límites y puede extenderse sin fin en ambas direcciones.
Tercer Postulado
Dado cualquier círculo y cualquier punto en su interior, se puede trazar un segmento de línea recta desde el centro del círculo hasta cualquier punto de su circunferencia.
Este postulado describe la relación entre el centro de un círculo y cualquier punto en su circunferencia.
Cuarto Postulado
Todos los ángulos rectos son iguales entre sí.
Este postulado afirma que los ángulos rectos, aquellos que miden 90 grados, son congruentes.
Quinto Postulado
Si una línea recta corta a dos líneas rectas y, en el mismo lado de la primera línea, los ángulos interiores suman menos de 180 grados, entonces las dos líneas se encuentran en ese lado al extenderlas.
Este postulado, también conocido como el Postulado de las Paralelas, establece las condiciones bajo las cuales dos líneas rectas son paralelas. Es el más famoso de los postulados de Euclides y la base de la geometría plana.
2. Aplicaciones de los Postulados de Euclides
Estos postulados permiten la construcción de teoremas fundamentales dentro de la geometría euclidiana. Algunos de los teoremas importantes derivados de estos postulados incluyen:
- Teorema de la semejanza de triángulos: Si dos triángulos tienen sus ángulos correspondientes congruentes, entonces los triángulos son semejantes.
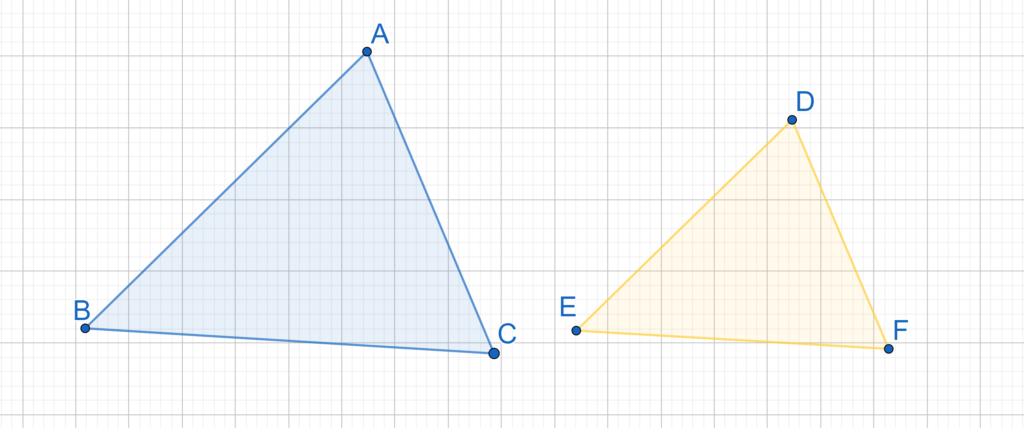
$$ \large \text{Si} \ \angle ABC = \angle DEF, \ \angle BCA = \angle EFD, \ \angle CAB = \angle FED, \ $$ $$ \large \text{entonces los triángulos ABC y DEF son semejantes.} $$
Teorema de Pitágoras: En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
$$ \Large c^2 = a^2 + b^2 $$
Teorema de la paralelogramo: El área de un paralelogramo se puede calcular como el producto de la base por la altura.
$$ \Large A = \text{base} \times \text{altura} $$
3. Importancia de los Postulados en la Geometría Euclidiana
Los postulados de Euclides son fundamentales para la construcción lógica de la geometría. A través de estos postulados, se derivan una vasta cantidad de teoremas que describen las propiedades de figuras geométricas como triángulos, círculos y polígonos. La geometría euclidiana se basa en la idea de que estos postulados son ciertas verdades universales, y cualquier figura geométrica se puede estudiar en función de estas leyes.
4. Conclusión
Los Postulados de Euclides siguen siendo la base de la geometría euclidiana y tienen una profunda influencia en la educación matemática. Son un conjunto de principios simples pero poderosos que nos permiten explorar y entender el espacio bidimensional de manera sistemática y lógica.