Permutaciones Simples en Lógica Matemática

Permutaciones Simples en Lógica Matemática

Las permutaciones simples son un concepto fundamental dentro de la combinatoria, un área clave de la lógica matemática. Este concepto se utiliza para contar el número de maneras en las que se pueden organizar un conjunto de elementos cuando el orden de los elementos sí importa. Las permutaciones simples son útiles en una amplia variedad de aplicaciones matemáticas, como en la teoría de probabilidades, la teoría de conjuntos y la resolución de problemas relacionados con el ordenamiento o la disposición de elementos.

Definición y Fórmula de las Permutaciones Simples

Una permutación simple de un conjunto de elementos es una disposición ordenada de esos elementos. En otras palabras, una permutación es cualquier arreglo de los elementos de un conjunto, donde el orden de los elementos sí tiene relevancia. La fórmula para calcular el número de permutaciones simples de un conjunto de elementos es:

$$ \Large P(n) = n! $$

Donde (denotado como factorial de ) es el producto de todos los números enteros positivos desde hasta . Es decir:

$$ \Large n! = n \times (n-1) \times (n-2) \times \dots \times 2 \times 1 $$

Propiedades de las Permutaciones Simples

Las permutaciones simples tienen varias propiedades interesantes que son útiles al resolver problemas de conteo y combinatoria:

1. Cantidad de Permutaciones: La cantidad de permutaciones de un conjunto de 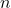elementos distintos es igual a 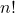. Por ejemplo, si tenemos 3 elementos 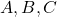, las permutaciones posibles son 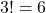, y las permutaciones son: .
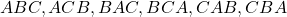2. Permutaciones de Elementos Identicos: Si algunos de los elementos del conjunto son idénticos, el número de permutaciones simples se ajusta dividiendo por el factorial de la cantidad de elementos idénticos. Por ejemplo, si tenemos un conjunto 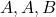, las permutaciones posibles son solo 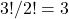, ya que los dos «A» son idénticos.
3. Factorial de un Número: El factorial de un número es un concepto central en las permutaciones. Para 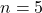, el número de permutaciones es . Esto indica que hay 120 formas diferentes de organizar un conjunto de 5 elementos distintos.

Ejemplos de Permutaciones Simples

1. Ejemplo 1: Si tenemos el conjunto 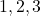, el número de permutaciones simples posibles es 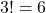. Las permutaciones son:
   • 123
   • 132
   • 213
   • 231
   • 312
   • 321
2. Ejemplo 2: Si tenemos el conjunto 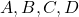, el número de permutaciones simples posibles es 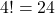. Las permutaciones incluyen:
   • ABCD
   • ABDC
   • ACBD
   • ACDB
   • ADBC
   • ADCB
   • … (y así sucesivamente)
3. Ejemplo 3: Si tenemos un conjunto de 3 letras donde dos son iguales, por ejemplo 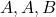, el número de permutaciones es 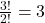. Las permutaciones son:
   • AAB
   • ABA
   • BAA

Aplicaciones de las Permutaciones Simples

Las permutaciones simples tienen una amplia gama de aplicaciones dentro de la lógica matemática, la teoría de conjuntos y la teoría de probabilidades. Algunas de las aplicaciones más comunes son:

1. Problemas de Ordenación: Las permutaciones se utilizan cuando necesitamos contar cuántas maneras diferentes podemos ordenar un conjunto de objetos. Esto puede aplicarse en problemas de organización de elementos en filas, tablas o listas.
2. Teoría de Probabilidades: En la teoría de probabilidades, las permutaciones simples se utilizan para calcular el número de resultados posibles de experimentos aleatorios cuando el orden de los resultados es importante. Por ejemplo, al lanzar una moneda varias veces y ordenar los resultados en diferentes secuencias.
3. Códigos y Combinaciones: En la teoría de códigos, las permutaciones son fundamentales para entender cómo se pueden organizar secuencias de símbolos. Esto es útil en criptografía y en la transmisión de información.

Relación con las Combinaciones

Es importante destacar que las permutaciones se diferencian de las combinaciones en que en las permutaciones el orden de los elementos sí importa, mientras que en las combinaciones no importa el orden. Por ejemplo, al seleccionar un subconjunto de elementos, la cantidad de combinaciones de elementos de un conjunto de elementos es distinta de la cantidad de permutaciones de esos mismos elementos.

Conclusión

Las permutaciones simples son una parte fundamental del estudio de la combinatoria en lógica matemática. Son esenciales para contar las diferentes formas en que los elementos de un conjunto pueden organizarse y tienen aplicaciones prácticas en probabilidad, teoría de conjuntos, y muchos otros campos de la matemática y las ciencias computacionales. El conocimiento de cómo calcular y aplicar permutaciones es crucial para resolver problemas que involucren el orden y la disposición de elementos.