En el campo de la combinatoria y enumeración, las permutaciones con repetición son un concepto crucial. A diferencia de las permutaciones simples, donde todos los elementos son distintos y se ordenan, las permutaciones con repetición se utilizan cuando algunos elementos pueden repetirse, lo que amplía las posibilidades de organización de los elementos. Este concepto es fundamental en la lógica matemática y en diversos campos como la teoría de códigos, la teoría de probabilidades y el análisis de sistemas complejos.
Definición de Permutaciones con Repetición
Una permutación con repetición es una organización de elementos de un conjunto en la que algunos de los elementos pueden repetirse. En este tipo de permutaciones, se considera el orden de los elementos, pero los elementos repetidos no se cuentan como elementos distintos.
La fórmula general para calcular el número de permutaciones con repetición cuando tenemos 
elementos disponibles y se seleccionan 
elementos es:
$$ \Large P(n, k) = n^k $$
Donde:
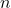- es el número de elementos disponibles para seleccionar.
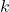- es el número de elementos a ordenar.
Esta fórmula refleja el hecho de que para cada uno de los lugares en la permutación, se pueden elegir uno de los elementos disponibles, y como el orden importa, se toma en cuenta todas las combinaciones posibles, incluidas aquellas en las que los elementos se repiten.
Propiedades de las Permutaciones con Repetición
Las permutaciones con repetición tienen propiedades importantes que son útiles para resolver una variedad de problemas en combinatoria. Algunas de estas propiedades incluyen:
- Consideración de Elementos Repetidos: A diferencia de las permutaciones sin repetición, en las permutaciones con repetición, los elementos pueden repetirse. Esto es útil en situaciones donde se desea realizar combinaciones de elementos que no necesariamente son únicos, como la creación de contraseñas, la asignación de recursos con repeticiones permitidas, etc.
- Orden Importante: Al igual que las permutaciones sin repetición, en las permutaciones con repetición, el orden de los elementos seleccionados sí importa. Esto implica que
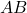es distinto de 
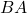, aunque ambos estén formados por los mismos elementos. - Aplicación en Problemas de Asignación: Las permutaciones con repetición son esenciales en problemas donde se deben asignar tareas o recursos a elementos con la posibilidad de repetirse, como asignar colores a objetos o elegir elementos de una lista con repeticiones permitidas.
Ejemplos de Permutaciones con Repetición
- Ejemplo 1: Si tenemos 3 colores
y queremos formar una secuencia de 2 colores (teniendo en cuenta que los colores pueden repetirse), el número de permutaciones con repetición es:
$$ \Large P(3, 2) = 3^2 = 9 $$
Las permutaciones posibles son: 
.
Ejemplo 2: Si tenemos 4 letras 
y queremos seleccionar 3 letras para formar una secuencia, el número de permutaciones con repetición es:
$$ \Large P(4, 3) = 4^3 = 64 $$
Las permutaciones posibles incluyen secuencias como: 
.
Ejemplo 3: Si se tienen 2 dígitos 
y queremos formar una secuencia de 4 dígitos, el número de permutaciones con repetición es:
$$ \Large P(2, 4) = 2^4 = 16 $$
Las permutaciones posibles son: 
.
Aplicaciones de las Permutaciones con Repetición
Las permutaciones con repetición tienen una variedad de aplicaciones en distintos campos de la lógica matemática y áreas aplicadas. Algunas de las aplicaciones clave incluyen:
- Códigos y Cifrado: En sistemas de codificación, como el diseño de contraseñas o códigos de acceso, las permutaciones con repetición se utilizan para calcular la cantidad de combinaciones posibles que un sistema de cifrado puede generar. Los elementos repetidos en un código pueden ser representados por números o caracteres.
- Teoría de la Información: En el análisis de la teoría de la información, las permutaciones con repetición son útiles para contar las secuencias de símbolos o bits en situaciones donde se permite que los símbolos se repitan.
- Problemas de Organización y Asignación: En situaciones de asignación de tareas o recursos con elementos repetidos (como asignar tareas a empleados o distribuir recursos entre clientes), las permutaciones con repetición ofrecen una manera de calcular las diversas formas en las que los elementos pueden ser organizados.
- Simulación y Análisis de Sistemas: Las permutaciones con repetición también son esenciales en la simulación de sistemas complejos, donde los elementos (como entradas o variables) pueden repetirse bajo diferentes condiciones de prueba, y el orden de las entradas es relevante para los resultados.
Conclusión
Las permutaciones con repetición son un concepto clave en combinatoria y en la teoría de enumeración dentro de la lógica matemática. Este concepto es fundamental para resolver problemas en los que se desea contar la cantidad de maneras de organizar elementos con repeticiones, como en la creación de contraseñas, la asignación de recursos, y muchos otros campos. Entender cómo calcular las permutaciones con repetición es esencial para abordar problemas combinatorios más complejos.