Números Irracionales

Números Irracionales en Aritmética Básica

Los números irracionales son aquellos que no pueden expresarse como el cociente de dos números enteros. Es decir, no pueden escribirse en la forma , donde y son enteros y . Su representación decimal es infinita y no periódica.

Definición y Representación

El conjunto de los números irracionales se denota generalmente como \(\mathbb{I}\) y se define como:

$$ \huge
\mathbb{I}=\left\{x\in\mathbb{R}|x\notin\mathbb{Q}\right\}
$$

Ejemplos de números irracionales:

• Raíces no exactas: 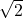,, 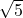(pues no tienen una expresión decimal finita o periódica).
• El número pi (\(\pi\)): Aproximadamente 3.14159265…, pero con una expansión infinita y sin patrón repetitivo.
• El número de Euler (\(e\)): Aproximadamente 2.71828182…, utilizado en cálculo y funciones exponenciales.
• La razón áurea (\(\varphi\)): 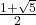, un número irracional asociado a la proporción áurea.

Propiedades de los Números Irracionales

Los números irracionales cumplen varias propiedades fundamentales:

1. No pueden representarse como fracción: No existe una expresión que sea exactamente igual a un número irracional.
2. Tienen una expansión decimal infinita y no periódica: No hay repetición cíclica en sus cifras decimales.
3. Son densos en la recta numérica: Entre dos números racionales siempre hay un número irracional y viceversa.
4. No son cerrados bajo suma o multiplicación:
   • La suma de dos irracionales puede ser racional .
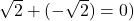   • La multiplicación de dos irracionales puede ser racional (ejemplo: .
5. Satisfacen propiedades algebraicas básicas: Se pueden sumar, restar, multiplicar y dividir bajo las reglas generales de la aritmética.

Comparación de Números Irracionales

Para comparar números irracionales, es útil aproximarlos en su forma decimal y compararlos como números reales.

Ejemplo: .

Aplicaciones de los Números Irracionales

Los números irracionales son fundamentales en:

• Geometría y trigonometría (\(\pi\) en el cálculo de circunferencias y áreas de círculos).
• Cálculo diferencial e integral (\(e\) en funciones exponenciales y logarítmicas).
• Diseño y arquitectura (razón áurea \(\varphi\)).
• Física y ciencias aplicadas (constantes irracionales en ecuaciones de la naturaleza).