Números Complejos en Aritmética Básica
En aritmética básica, los números complejos aparecen como una extensión del sistema de los números reales, permitiendo la solución de ecuaciones que no tienen soluciones reales. Su comprensión es fundamental para el desarrollo de conceptos en álgebra y otras ramas de las matemáticas.
Definición de los Números Complejos
Un número complejo es un número de la forma:
$$ \Huge z = a + bi $$
donde:
y 
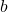son números reales,
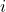es la unidad imaginaria, definida por 
.
Si 
, el número complejo se reduce a un número real. Si 
y 
, el número es puramente imaginario.
Operaciones Básicas con Números Complejos
Las operaciones con números complejos siguen reglas similares a las de los números reales, con la particularidad de que 
siempre se reemplaza por 
.
Suma y Resta
Dados dos números complejos 
y 
, se tiene:
$$ \huge z_1 + z_2 = (a+c) + (b+d)i $$ $$ \huge z_1 − z_2 = (a−c) + (b−d)i $$
La suma y la resta se hacen componente a componente.
Multiplicación
Para multiplicar dos números complejos:
$$ \huge (a + bi)(c + di) = ac + adi + bci + bdi^2 $$
$$ \Large \text{Como } i^2 = -1 \text{, esto se simplifica a:} $$
$$ \huge (a + bi)(c + di) = (ac – bd) + (ad + bc)i $$
División
Para dividir 
, se multiplica el numerador y denominador por el conjugado de 
, que es 
:
$$ \huge \frac{(a+bi)(c-di)}{(c+di)(c-di)} $$
El denominador se convierte en un número real:
$$ \huge c^2 + d^2 $$
El resultado final es:
$$ \huge \frac{(ac + bd) + (bc – ad)i}{c^2 + d^2} $$
https://chatgpt.com/canvas/shared/67d46c479b8c819195afd334f82031f6
Conjugado de un Número Complejo
El conjugado de 
es 
. Su principal utilidad es facilitar operaciones como la división y encontrar módulos de números complejos.
Módulo de un Número Complejo
El módulo de 
se denota como 
y se calcula con la fórmula:
$$ \huge |z| = \sqrt{a^2 + b^2} $$
Este valor representa la distancia del número complejo al origen en el plano complejo.
Conclusión
Los números complejos amplían el sistema numérico real y permiten operar con raíces de números negativos. Su comprensión en aritmética básica es clave para el estudio posterior del álgebra y análisis matemático.
