Módulo y Residuo en Aritmética Modular
En Aritmética Modular y Congruencias, el concepto de módulo y residuo es esencial para resolver problemas relacionados con divisibilidad y divisores. La aritmética modular es una forma de realizar cálculos en un sistema numérico que «se reinicia» después de alcanzar un cierto valor. Este enfoque es particularmente útil en teoría de números, criptografía, y otras áreas de las matemáticas.
1. ¿Qué es el Módulo?
El módulo de un número se refiere a la operación matemática que nos dice cuánto «sobra» o «resta» cuando un número se divide entre otro. Es una forma de representar el «resto» de una división. Se denota generalmente como \( a \mod n\), donde \(a\) es el número a dividir, y \(n\) es el divisor.
La operación de módulo da el residuo que queda después de dividir un número \(a\) entre \(n\). Es decir:
$$ \huge a \mod n = r $$
donde 
es el residuo de la división de 
por 
.
Ejemplo:
Si tenemos el número \(17\) y lo dividimos entre \(5\): 
Por lo tanto, el residuo es 2, y podemos escribir:
$$ 17 \mod 5 = 2 $$
2. Residuo de una División
El residuo es la cantidad que queda después de realizar una división, y está relacionado directamente con el concepto de módulo. El residuo es siempre un número entre 0 y 
, donde es el divisor.
Ejemplo:
Si dividimos 20 entre 6: $$ \large 20 \div 6 = 3 \quad \text{(cociente)} \quad 20 – (6 \times 3) = 2 $$
El residuo es 2, y podemos decir que: $$ \large 20 \mod 6 = 2 $$
3. Propiedades del Módulo
La operación de módulo tiene varias propiedades que son muy útiles en la resolución de problemas matemáticos, especialmente cuando trabajamos con congruencias.
3.1 Propiedad de la Conmutatividad
La operación de módulo no es conmutativa. Es decir, 
no es lo mismo que 
, a menos que 
.
3.2 Propiedad de la Distributividad
La operación de módulo es distributiva con respecto a la suma y la multiplicación:
- \( (a + b) \mod n = [(a \mod n) + (b \mod n)] \mod n \)
- \( (a \times b) \mod n = [(a \mod n) \times (b \mod n)] \mod n \)
Ejemplo:
\(\text{Si }a=13, b=8, \text{ y } n = 5,\text{ entonces: }\)
\((13 + 8) \mod 5 = 21 \mod 5 = 1 \) y \((13 \mod 5 + 8 \mod 5) \mod 5 = (3 + 3) \mod 5 = 6 \mod 5 = 1\)
4. Congruencias y su Relación con el Módulo
Una congruencia es una forma de expresar la igualdad de residuos en una división. Decimos que dos números y 
son congruentes módulo si tienen el mismo residuo al dividirlos por . Se denota como:
$$ \large a \equiv b \mod n $$
Esto significa que al dividir y entre , los dos números tienen el mismo residuo.
Ejemplo:
Si \(a=17\) y \(b=2\), y \(n=5\), entonces:
$$ \large 17 \div 5 = 3 \quad \text{(cociente)} \quad \text{y residuo} = 2 $$ $$ \large 2 \div 5 = 0 \quad \text{(cociente)} \quad \text{y residuo} = 2 $$
Como los restos son iguales, podemos escribir:
$$ \large 17 \equiv 2 \mod 5 $$
5. Propiedades de las Congruencias
Las congruencias tienen varias propiedades que las hacen muy útiles en matemáticas:
- Reflexividad:
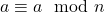
- Simetría: Si
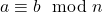, entonces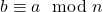 
- Transitivida: Si 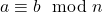y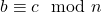
, entonces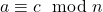 
- Adición y multiplicación: Si 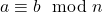y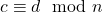
, entonces:
6. Ejercicios Prácticos
Ejercicio 1:
Calcula 
.
Solución:
Dividimos 47 entre 6:
$$ \large 47 \div 6 = 7 \quad \text{(cociente)} \quad 47 – (6 \times 7) = 5 $$
Por lo tanto, el residuo es 5, y:
$$ \large 47 \mod 6 = 5 $$
Ejercicio 2:
Verifica si \(23 \equiv 4 \mod 7\).
Solución:
Dividimos 23 entre 7:
$$ \large 23 \div 7 = 3 \quad \text{(cociente)} \quad 23 – (7 \times 3) = 2 \text{(resto)} $$
Dividimos 4 entre 7:
$$ \large 4 \div 7 = 0 \quad \text{(cociente)} \quad 4 – (7 \times 0) = 4 \text{(resto)} $$
Como los restos son diferentes, podemos concluir que:
$$ \large 23 \not\equiv 4 \mod 7 $$
7. Conclusión
El concepto de módulo y residuo es fundamental en Aritmética Modular y Congruencias. La habilidad para trabajar con estos conceptos permite resolver una variedad de problemas en teoría de números, criptografía y áreas relacionadas. Comprender cómo calcular y aplicar módulos y congruencias es esencial para desarrollar una comprensión más profunda de las matemáticas.
