Mínimo Común Múltiplo (MCM) en Aritmética
El Mínimo Común Múltiplo (MCM) es un concepto importante en Aritmética que se utiliza para encontrar el menor múltiplo común de dos o más números. Es fundamental en la resolución de problemas relacionados con fracciones, sincronización de ciclos repetitivos y otros cálculos matemáticos. En este post, exploraremos cómo calcular el MCM y su relevancia en las matemáticas.
1. Definición de Mínimo Común Múltiplo (MCM)
El Mínimo Común Múltiplo (MCM) de dos o más números es el menor número positivo que es múltiplo de cada uno de los números dados. Es decir, es el menor número que puede ser dividido sin residuo por cada uno de los números dados.
Por ejemplo, si tenemos los números 6 y 8, queremos encontrar el menor número que sea múltiplo de ambos.
2. Métodos para Calcular el MCM
Existen varios métodos para calcular el MCM de dos o más números. A continuación, describimos los dos métodos más comunes: el método de descomposición en factores primos y el método de los múltiplos comunes.
2.1 Método de Descomposición en Factores Primos
Este método consiste en descomponer cada número en sus factores primos y luego tomar todos los factores primos con sus mayores exponentes.
Ejemplo:
Vamos a calcular el MCM de 6 y 8.
- La descomposición en factores primos de 6 es:
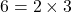
- La descomposición en factores primos de 8 es:
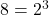
Para encontrar el MCM, tomamos todos los factores primos con los mayores exponentes:
- El mayor exponente de
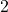es 
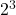. - El mayor exponente de
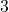es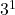 
.
Por lo tanto, el MCM es:
$$ \Large \text{MCM}(6, 8) = 2^3 \times 3^1 = 24 $$
2.2 Método de los Múltiplos Comunes
En este método, calculamos los múltiplos de cada número y luego seleccionamos el menor múltiplo común.
Ejemplo:
- Múltiplos de 6:
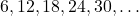
- Múltiplos de 8:
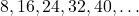
El menor múltiplo común es 
, por lo que el MCM de 6 y 8 es 24.
$$ \Large \text{MCM}(6, 8) = 24 $$
3. Propiedades del MCM
El MCM tiene varias propiedades útiles que facilitan su cálculo y aplicación:
- MCM de un número con 1: El MCM de cualquier número
y 1 es siempre el número , es decir:
$$ \Large \text{MCM}(a, 1) = a $$
- MCM de un número consigo mismo: El MCM de cualquier número consigo mismo es el propio número, es decir:
$$ \Large \text{MCM}(a, a) = a $$
- MCM de dos números primos entre sí: Si dos números son primos entre sí, es decir, no tienen factores primos comunes, su MCM es el producto de los dos números:
4. MCM de Tres o Más Números
Para encontrar el MCM de tres o más números, aplicamos el mismo procedimiento. Primero calculamos el MCM de dos números, luego usamos el resultado para calcular el MCM con el siguiente número, y así sucesivamente.
Ejemplo:
Vamos a encontrar el MCM de 4, 6 y 8.
- El MCM de 4 y 6 es 12 (de acuerdo con los pasos descritos anteriormente).
- Ahora calculamos el MCM de 12 y 8. La descomposición en factores primos de 12 es
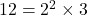y la de 8 es 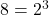. Tomamos los factores primos con los mayores exponentes:
$$ \Large \text{MCM}(12, 8) = 2^3 \times 3 = 24 $$
Por lo tanto:
$$ \Large \text{MCM}(4, 6, 8) = 24 $$
5. Aplicaciones del MCM
El MCM tiene diversas aplicaciones en las matemáticas y la resolución de problemas, tales como:
- Simplificación de fracciones: El MCM se usa para encontrar el mínimo común denominador (MCD) al sumar o restar fracciones con denominadores diferentes. Para sumar o restar fracciones con denominadores \(a\) y \(b\), usamos el MCM para encontrar el denominador común más pequeño, y luego ajustamos las fracciones.
$$ \Large \frac{a}{b} + \frac{c}{d} = \frac{a \cdot \text{MCM}(b, d)}{b \cdot \text{MCM}(b, d)} + \frac{c \cdot \text{MCM}(b, d)}{d \cdot \text{MCM}(b, d)} $$
- Problemas de sincronización: El MCM es útil cuando necesitamos sincronizar eventos que ocurren en intervalos repetitivos. Por ejemplo, si dos procesos se repiten cada 4 y 6 unidades de tiempo, el MCM nos dirá cada cuántas unidades de tiempo ambos procesos se alinearán.
- Resolución de problemas con ciclos repetitivos: En situaciones donde dos o más eventos ocurren en ciclos repetitivos, el MCM se utiliza para determinar el intervalo en el que se repiten ambos eventos simultáneamente.
Conclusión
El Mínimo Común Múltiplo (MCM) es un concepto clave en Aritmética, esencial para la resolución de problemas que involucran fracciones, múltiplos y ciclos repetitivos. Comprender cómo calcular el MCM y sus aplicaciones prácticas es fundamental para desarrollar una sólida comprensión de las matemáticas.
