Lógica Paraconsistente

Lógica Paraconsistente

La lógica paraconsistente es una rama de la lógica no clásica que se caracteriza por su capacidad para manejar contradicciones de manera controlada, sin que ello conduzca a una explosión lógica. En la lógica clásica, una contradicción implica que cualquier proposición puede ser derivada a partir de ella, lo que hace que el sistema sea inconsistente y poco útil en situaciones con contradicciones. En contraste, la lógica paraconsistente permite que coexistan contradicciones en un sistema sin que estas comprometan su validez o capacidad de razonamiento.

En este post, exploraremos los principios fundamentales de la lógica paraconsistente, sus características principales, y cómo se aplica en la teoría de la lógica matemática.

Principios Fundamentales de la Lógica Paraconsistente

La lógica paraconsistente permite que una teoría o sistema lógico sea inconsistente en algunos casos, pero sin que esta inconsistencia cause la explosión de derivaciones absurdas. Es decir, una contradicción no lleva a la contradicción generalizada que ocurre en la lógica clásica, donde cualquier proposición derivada de una contradicción es también verdadera.

A continuación, se describen algunos de los principios fundamentales que definen la lógica paraconsistente:

• No explosión: Una de las características más distintivas de la lógica paraconsistente es que no se permite la explosión lógica. En la lógica clásica, si una contradicción es aceptada, cualquier proposición puede ser derivada de ella, lo que hace que el sistema pierda su utilidad. En la lógica paraconsistente, se evita esta explosión, permitiendo que la contradicción no se propague.
• Contradicciones toleradas: En los sistemas paraconsistentes, las contradicciones pueden ser parte del sistema sin invalidarlo. Esto significa que una proposición 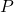y su negación 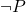pueden ser ambas verdaderas en el sistema, pero esto no lleva a que cualquier otra proposición sea considerada verdadera.
• Operadores lógicos: Los operadores lógicos en la lógica paraconsistente pueden comportarse de manera diferente que en la lógica clásica, adaptándose para manejar contradicciones sin producir resultados indeseados. Por ejemplo, la conjunción y la disyunción en la lógica paraconsistente pueden definirse de manera que preserven la integridad del sistema incluso cuando se enfrentan a contradicciones.

Comparación con la Lógica Clásica

En la lógica clásica, la ley de la contradicción establece que una proposición y su negación no pueden ser ambas verdaderas al mismo tiempo. Esto implica que si es verdadera, entonces debe ser falsa, y viceversa. En la lógica paraconsistente, sin embargo, se permite que una proposición y su negación puedan ser verdaderas al mismo tiempo, sin que esto cause una explosión lógica.

Por ejemplo, si en un sistema clásico tenemos que y , podemos derivar de una contradicción. Sin embargo, en un sistema paraconsistente, la contradicción no lleva necesariamente a la conclusión de manera indiscriminada.

Propiedades de la Lógica Paraconsistente

Las lógicas paraconsistentes se caracterizan por algunas propiedades claves que las distinguen de las lógicas tradicionales:

• Negación paraconsistente: La negación en la lógica paraconsistente no genera una explosión. En lugar de asumir que la negación de una contradicción produce todas las proposiciones como verdaderas, la negación paraconsistente puede estar restringida a un conjunto más limitado de derivaciones.
• Conjunción paraconsistente: La conjunción en un sistema paraconsistente puede ser definida de manera que no se ve afectada por contradicciones. Por ejemplo, en un sistema clásico, 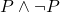sería una contradicción y no tendría valor de verdad. En la lógica paraconsistente, este tipo de conjunción puede ser permitida, pero bajo una interpretación que no genere caos en el sistema.
• Disyunción paraconsistente: Similarmente, la disyunción en un sistema paraconsistente puede ser tratada de una manera que no conduzca a inferencias descontroladas. Por ejemplo, 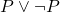podría ser aceptada en un contexto paraconsistente sin la necesidad de que toda proposición sea derivable.

Aplicaciones de la Lógica Paraconsistente

La lógica paraconsistente tiene aplicaciones en varios campos, especialmente donde las contradicciones no son solo inevitables, sino también útiles:

1. Inteligencia Artificial: La lógica paraconsistente se utiliza en la inteligencia artificial, particularmente en sistemas de razonamiento no monótono donde se enfrentan situaciones con información contradictoria. Por ejemplo, en sistemas de diagnóstico, puede ser necesario manejar información que parece contradictoria debido a la falta de datos completos.
2. Teoría de Bases de Datos: En bases de datos, especialmente en aquellas que gestionan grandes cantidades de información, puede haber contradicciones o datos inconsistentes. La lógica paraconsistente permite tratar estos casos sin perder la validez de las consultas o de la integridad del sistema.
3. Filosofía y Lógica Formal: La lógica paraconsistente también ha sido utilizada en debates filosóficos y estudios sobre el razonamiento en contextos conflictivos, como en la dialéctica o la lógica de contraposiciones.
4. Cálculos de Lógica y Verificación de Programas: En la verificación de programas, se pueden presentar contradicciones en las especificaciones de un programa o en sus ejecuciones. La lógica paraconsistente permite abordar estos problemas sin caer en inconsistencias generalizadas, permitiendo que el sistema sea robusto ante ciertas contradicciones.

Conclusión

La lógica paraconsistente ofrece una poderosa alternativa a la lógica clásica, permitiendo manejar contradicciones de manera controlada y útil, sin que estas lleven a una explosión lógica que desestabilice el sistema. Con aplicaciones en inteligencia artificial, filosofía, bases de datos, y más, la lógica paraconsistente es una herramienta valiosa para trabajar con sistemas en los que las contradicciones no son solo posibles, sino que deben ser aceptadas y gestionadas de manera efectiva.