Lógica Modal y Sistemas Kripke
La lógica modal es una extensión de la lógica clásica que introduce conceptos como la necesidad y la posibilidad, representadas por los operadores modales 
(necesariamente) y 
(posiblemente). A diferencia de la lógica clásica, donde cada proposición es simplemente verdadera o falsa, en la lógica modal estas proposiciones pueden ser evaluadas dentro de diferentes «mundos posibles». Estos mundos posibles representan diferentes estados de conocimiento, circunstancias o realidades, lo que agrega flexibilidad y aplicabilidad en áreas como la filosofía, la informática y la inteligencia artificial.
En este post, exploraremos los sistemas Kripke, un enfoque fundamental en la semántica de la lógica modal, que proporciona una interpretación formal de los operadores modales dentro de un marco lógico.
Lógica Modal: Definición y Operadores
La lógica modal se caracteriza por dos operadores principales:
- Necesidad
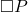: Significa que una proposición 
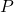es verdadera en todos los mundos posibles. - Posibilidad
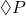: Significa que una proposición 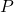es verdadera en al menos uno de los mundos posibles.
Estas modalidades permiten expresar conceptos complejos, como la certeza, la posibilidad de eventos futuros, o la verdad en diferentes contextos de conocimiento o tiempo. La interpretación formal de estas modalidades depende de la relación entre los mundos posibles.
Sistemas Kripke: Semántica de la Lógica Modal
La semántica de la lógica modal se formaliza a través de los sistemas Kripke, que son un modelo de interpretación basado en la idea de mundos posibles y relaciones de accesibilidad entre ellos. En un sistema Kripke, la interpretación de la lógica modal se organiza de la siguiente manera:
- Mundo posible: Un conjunto de proposiciones que pueden ser verdaderas o falsas en un mundo específico.
- Relación de accesibilidad: Una relación
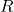entre los mundos posibles que describe cómo un mundo puede acceder a otro. Si 
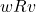, esto significa que el mundo posible 
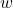puede acceder al mundo posible 
. - Valuación: Una asignación de valores de verdad a las proposiciones dentro de cada mundo posible.
La semántica de los sistemas Kripke permite interpretar las fórmulas modales. Por ejemplo, la fórmula se interpreta como «para todo mundo accesible desde el mundo actual, es verdadero», y se interpreta como «existe al menos un mundo accesible desde el mundo actual donde es verdadero».
Propiedades de los Sistemas Kripke
Los sistemas Kripke varían en función de las propiedades de la relación de accesibilidad . Dependiendo de estas propiedades, se pueden obtener diferentes sistemas modales, que incluyen:
- Reflexividad: Un mundo es accesible desde sí mismo, es decir,
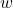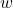. - Simetría: Si un mundo puede acceder a , entonces puede acceder a , es decir,
. - Transitividad: Si un mundo 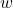puede acceder a , y puede acceder a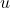
, entonces 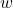puede acceder a 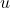, es decir, 
.
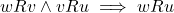Cada una de estas propiedades da lugar a diferentes lógicas modales, que se conocen como sistemas modales. Algunas de las lógicas más importantes incluyen:
- Lógica S5: La relación de accesibilidad es reflexiva, simétrica y transitiva, lo que implica que todos los mundos son accesibles entre sí. Esto implica que todo lo que es posible también es necesariamente posible.
- Lógica K: Es el sistema modal más básico, en el que solo se requiere que la relación de accesibilidad sea reflexiva.
Aplicaciones de la Lógica Modal
La lógica modal es extremadamente útil en varios campos, incluyendo:
- Filosofía: Para abordar cuestiones como la verdad, la necesidad y la posibilidad en diferentes mundos posibles, como en el análisis de la necesidad de eventos o la posibilidad de futuros alternativos.
- Inteligencia artificial y computación: En la verificación de programas, la lógica modal se utiliza para especificar las propiedades de sistemas interactivos y para razonar sobre sistemas que evolucionan en el tiempo.
- Lingüística: En el análisis semántico de lenguajes naturales, especialmente en el contexto de las oraciones que expresan necesidad o posibilidad.