Lógica Intuicionista

Tabla de contenidos

La lógica intuicionista es una forma de lógica no clásica que se fundamenta en la concepción de que el conocimiento matemático debe ser constructivo. En lugar de asumir que las proposiciones son simplemente verdaderas o falsas, la lógica intuicionista enfatiza que la verdad de una proposición debe ser demostrable mediante una construcción explícita. Esta visión se aleja de la lógica clásica, donde se admite la ley del tercero excluido (es decir, una proposición es verdadera o falsa) sin la necesidad de un procedimiento constructivo.

En este post, exploraremos los principios fundamentales de la lógica intuicionista, sus diferencias con la lógica clásica, y cómo se aplica en el campo de la lógica matemática.

Principios Fundamentales de la Lógica Intuicionista

La lógica intuicionista se diferencia de la lógica clásica en varios aspectos fundamentales. Los principales elementos que caracterizan la lógica intuicionista incluyen:

Negación Constructiva: En lógica intuicionista, la negación de una proposición no se interpreta simplemente como su falsedad. En lugar de eso, afirmar que una proposición 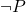$\neg P$ es verdadera significa que se ha demostrado que 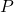$P$ lleva a una contradicción. Esto implica que no podemos simplemente asumir la negación de una proposición sin una construcción que lo justifique.
Ley del Tercero Excluido: En la lógica clásica, la ley del tercero excluido establece que para cualquier proposición 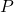$P$ , siempre es cierto que 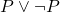$P \lor \neg P$ . Sin embargo, en lógica intuicionista, esta ley no se acepta como válida, ya que no siempre es posible construir una prueba de que una proposición es verdadera o su negación lo es. Es decir, no podemos afirmar que 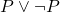$P \lor \neg P$ sin una construcción efectiva de la verdad de 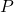$P$ o $\neg P$ .
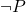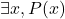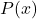Existencia Constructiva: Para afirmar que existe un objeto con una propiedad específica, en lógica intuicionista es necesario presentar una construcción explícita de dicho objeto. En términos de cuantificadores, esto significa que para afirmar $\exists x , P(x)$ , debe existir una demostración constructiva de la existencia de algún $x$ tal que $P(x)$ sea verdadero.
Implica Constructiva: La implicación en la lógica intuicionista es también constructiva. Para afirmar una implicación 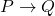$P \rightarrow Q$ , no solo debemos aceptar que si 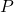$P$ es verdadero, entonces 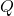$Q$ también lo será, sino que debe existir una método constructivo para convertir una prueba de 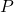$P$ en una prueba de $Q$ .

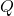Comparación con la Lógica Clásica

La diferencia más destacada entre la lógica intuicionista y la lógica clásica radica en la interpretación de las leyes de la lógica. Mientras que en la lógica clásica las leyes como el tercero excluido y la doble negación se consideran válidas sin necesidad de una construcción directa, en la lógica intuicionista estas leyes no se aceptan sin una justificación constructiva.

Doble Negación: En lógica clásica, la doble negación es una tautología, es decir, 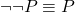$\neg \neg P \equiv P$ . Sin embargo, en lógica intuicionista, esta equivalencia no siempre es válida, ya que la doble negación solo garantiza la inexistencia de una contradicción, no la verdad de $P$ .

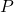Aplicaciones de la Lógica Intuicionista

La lógica intuicionista tiene aplicaciones en varias áreas de las matemáticas y la informática:

Matemáticas Constructivas: La lógica intuicionista es la base de las matemáticas constructivas, un enfoque que requiere que todas las entidades matemáticas sean construidas explícitamente. Este enfoque tiene aplicaciones importantes en la teoría de la computación y en la formulación de algoritmos constructivos.
Lógica de Programación: En la informática, la lógica intuicionista se aplica en el diseño de lenguajes de programación que requieren que las pruebas de los programas sean constructivas, lo que garantiza la existencia de soluciones efectivas.
Teoría de Categorías: La lógica intuicionista también ha influido en el desarrollo de la teoría de categorías, especialmente en su aplicación a la teoría de la computación y el análisis de programas.

Conclusión

La lógica intuicionista ofrece una visión constructiva de las proposiciones matemáticas, en contraste con la lógica clásica. En lugar de asumir que las proposiciones son verdaderas o falsas de manera inmediata, la lógica intuicionista exige que la verdad se construya mediante procedimientos explícitos. Este enfoque tiene implicaciones profundas en la forma en que entendemos la verdad matemática y cómo construimos el conocimiento en diversos campos de las ciencias exactas.