Lógica Difusa

Tabla de contenidos

La lógica difusa (o lógica fuzzy) es una extensión de la lógica clásica que permite manejar la incertidumbre y la imprecisión, características inherentes en muchas situaciones del mundo real. En la lógica clásica, las proposiciones son evaluadas como verdaderas o falsas, es decir, su valor de verdad está restringido a 0 o 1. En cambio, en la lógica difusa, los valores de verdad son un continuum que puede tomar cualquier valor dentro del intervalo $[0, 1]$ , lo que permite representar grados de verdad en lugar de simples afirmaciones de verdad absoluta.

En este post, exploraremos los principios fundamentales de la lógica difusa, su funcionamiento en la teoría de la lógica matemática, y sus aplicaciones en diferentes áreas como la inteligencia artificial, la toma de decisiones y el control automático.

Principios Fundamentales de la Lógica Difusa

En la lógica difusa, las proposiciones no se limitan a ser simplemente verdaderas o falsas, sino que pueden ser parcialmente verdaderas, permitiendo modelar la incertidumbre y la imprecisión. Algunas de las características clave de la lógica difusa incluyen:

Valores de verdad continuos: A diferencia de la lógica clásica, donde el valor de verdad de una proposición es un valor binario (verdadero o falso), en la lógica difusa el valor de verdad puede ser cualquier número real dentro del intervalo $[0, 1]$ . Esto permite representar la gradualidad de las propiedades, como «casi verdadero» o «bastante falso».
Operadores difusos: Los operadores lógicos tradicionales (como AND, OR, NOT) también se modifican en la lógica difusa para operar sobre valores continuos. Por ejemplo, la conjunción difusa (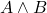) y la disyunción difusa (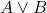) se definen de manera diferente que en la lógica clásica. En lógica difusa:
- La conjunción se define como:

$$ \Large A \land B = \min(A, B) $$

La disyunción se define como:

$$ \Large A \lor B = \max(A, B) $$

Estos operadores permiten combinar los valores de verdad de manera flexible según el grado de pertenencia a una categoría.

Negación difusa: La negación en lógica difusa se define de manera similar a la de la lógica clásica, pero tomando en cuenta el valor de verdad continuo. Se puede definir como:
$\neg A = 1 - A$
Esto refleja cómo un valor de verdad más alto se invierte hacia un valor menor, lo que permite una negación proporcional en lugar de absoluta.

Comparación con la Lógica Clásica

En la lógica clásica, los valores de verdad son estrictamente binarios, mientras que en la lógica difusa, los valores de verdad pueden ser cualquier número real entre 0 y 1. Esta diferencia es clave para la modelización de sistemas en los que los límites entre las categorías son borrosos o no bien definidos.

Por ejemplo, si en lógica clásica decimos que «el sistema está encendido», esto se traduce a un valor de verdad de 1 (verdadero) o 0 (falso). En cambio, en lógica difusa, podemos tener valores como 0.7, lo que indicaría que el sistema está «parcialmente encendido».

Operaciones en Lógica Difusa

En lógica difusa, las operaciones lógicas son generalmente definidas de la siguiente manera:

Conjunción (AND difusa): Se utiliza el mínimo de los valores de verdad de los dos operandos. Si 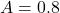$A = 0.8$ y $B = 0.6$ , entonces $A \land B = \min(0.8, 0.6) = 0.6$ .
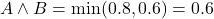Disyunción (OR difusa): Se utiliza el máximo de los valores de verdad de los dos operandos. Si 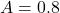$A = 0.8$ y $B = 0.6$ , entonces $A \lor B = \max(0.8, 0.6) = 0.8$ .
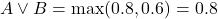Negación difusa: La negación de un valor de verdad 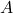$A$ es simplemente 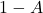$1 - A$ , lo que invierte el grado de verdad. Si 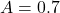$A = 0.7$ , entonces $\neg A = 1 - 0.7 = 0.3$ .

Aplicaciones de la Lógica Difusa

La lógica difusa tiene una amplia gama de aplicaciones en diversas áreas:

Control Difuso: Uno de los usos más conocidos de la lógica difusa es en el control difuso, donde se utiliza para modelar sistemas que requieren tomar decisiones basadas en información imprecisa. Un ejemplo típico es el control de temperatura en sistemas de calefacción o aire acondicionado, donde se toman decisiones basadas en «grados de calentamiento» y «necesidad de ajuste».
Inteligencia Artificial: En la inteligencia artificial, la lógica difusa se emplea para representar información ambigua o incierta en sistemas de razonamiento automático. Los sistemas basados en lógica difusa pueden manejar mejor la incertidumbre inherente a las tareas de diagnóstico, clasificación y toma de decisiones.
Tomar Decisiones: La lógica difusa se aplica en el análisis de decisiones complejas, donde las opciones no se dividen claramente entre «sí» o «no». Por ejemplo, puede ser utilizada para evaluar riesgos financieros, diagnósticos médicos, y predicciones de comportamiento de sistemas dinámicos.
Reconocimiento de Patrones: En el campo del procesamiento de imágenes y reconocimiento de patrones, la lógica difusa ayuda a clasificar imágenes en categorías difusas, lo que permite una mayor flexibilidad al identificar patrones que no encajan perfectamente en una categoría específica.

Conclusión

La lógica difusa proporciona un marco matemático robusto para manejar la incertidumbre y la imprecisión de manera continua, lo que la convierte en una herramienta útil para modelar sistemas en los que los límites son difusos o difíciles de definir. Con aplicaciones en áreas tan variadas como la inteligencia artificial, el control automático y la toma de decisiones, la lógica difusa ha demostrado ser esencial para tratar situaciones en las que la lógica clásica no es suficiente.

Etiquetas Sugeridas:

lógica difusa, lógica matemática, lógica no clásica, incertidumbre, control difuso, inteligencia artificial, toma de decisiones, operadores difusos, razonamiento difuso, teoría de conjuntos difusa, procesamiento de imágenes, reconocimiento de patrones, lógica continua, sistemas difusos, lógica fuzzy,