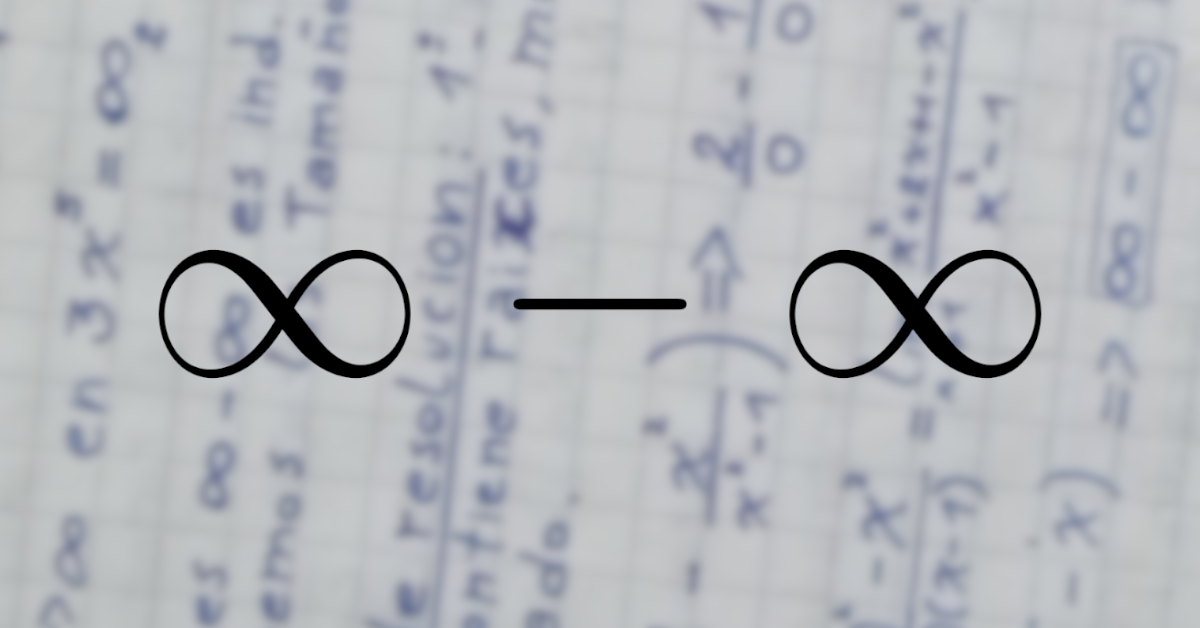¿Por qué es indeterminado?
Si \(x\to \infty\) en \(x^{3}\to \infty_{1}\) ; intuitivamente se ve que \(\infty _{1}<\infty _{2}\)
y \(x\to \infty\) en \(3x^{5}=\infty _{2}\)
Entonces \(\infty – \infty\) es indeterminación matemática porque no sabemos los tamaños de los infinitos.
Modo de resolución:
- Unificar la expresión
- Si contiene raíces, multiplicarlos por el conjugado.
Ejemplo N°1
$$ \displaystyle\lim_{x\to 1} \left ( \frac{x+1}{x-1}-\frac{x^{2}}{x^{2}-1} \right ) \Rightarrow\frac{2}{0}-\frac{1}{0}\Rightarrow\infty-\infty \; \; \; {{\color{red}{indeterminado}}} $$
Modo 1°
$$ \displaystyle\lim_{x\to 1} \frac{x+1}{x-1}-\frac{x^{2}}{x^{2}-1} = \lim_{x\to 1} \frac{x^{2}+2x+1-x^{2}}{x^{2}-1}= \lim_{x\to 1} \frac{2x+1}{x^{2}-1}=\frac{3}{0}\Rightarrow\infty$$
Ejemplo N°2
$$ \displaystyle\lim_{x\to \infty} \left ( \sqrt{x^{2}-1}-x \right ) \Rightarrow\infty-\infty \; \; \; {{\color{red}{indeterminado}}} $$
$$ \displaystyle\lim_{x\to \infty} \frac{(\sqrt{x^{2}-1}-x) \cdot (\sqrt{x^{2}-1}+x)}{(\sqrt{x^{2}-1}+x)} \Rightarrow \lim_{x\to \infty} \frac{(x^{2}-1)-x^{2}}{\sqrt{x^{2}+x}} \Rightarrow \lim_{x \to \infty} \frac{-1}{\sqrt{x^{2}-1}+x} = \frac{-1}{\infty} = 0 $$