Grandes Cardinales en la Teoría de Conjuntos
En el ámbito de la teoría de conjuntos, los grandes cardinales son un tema central que profundiza en la jerarquía infinita de los números cardinales. Estos cardinales son fundamentales para entender la estructura de los conjuntos infinitos y se encuentran más allá de los cardinales estándar utilizados para describir la cardinalidad de conjuntos finitos o de los conjuntos numerables.
Definición de Cardinalidad y Cardinales Infinitos
En términos simples, un cardinal es una medida de la «tamaño» de un conjunto, que nos dice cuántos elementos tiene. Para conjuntos finitos, el cardinal es simplemente un número natural. Sin embargo, cuando se trata de conjuntos infinitos, la teoría de cardinalidad se complica. La noción básica de cardinalidad infinita comienza con el cardinal de los números naturales, que se denota como 
, y representa el tamaño del conjunto de los números naturales, el conjunto más pequeño de los conjuntos infinitos.
Cardinales Sucesivos
A partir del cardinal , los cardinales sucesivos se denotan como 
, y cada uno de estos cardinales representa conjuntos más grandes que . Sin embargo, estos cardinales aún no son considerados «grandes cardinales», ya que pertenecen a una jerarquía más baja.
Definición de Grandes Cardinales
Un gran cardinal es un número cardinal que posee propiedades especiales que lo hacen destacar en la jerarquía de cardinales. Algunos ejemplos de grandes cardinales incluyen:
- Cardinales Inaccesibles: Un cardinal
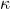es inaccesible si es un cardinal regular (no puede ser expresado como la unión de menos de 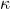conjuntos de cardinalidad menor que 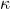) y si no hay un conjunto de cardinalidad menor que 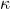cuya estructura sea suficientemente rica como para generar 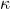. - Cardinales Mahlo: Un cardinal 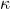es Mahlo si el conjunto de subconjuntos de cardinalidad menor que 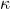que son cerrados bajo operaciones de conjunto es «grande» en algún sentido técnico. Esto implica que los cardinales Mahlo están muy por encima de los cardinales accesibles.
- Cardinales de Woodin: Estos cardinales son una extensión de los cardinales inaccesibles y están relacionados con las propiedades del espacio de fórmulas en modelos de conjuntos. Los cardinales de Woodin tienen implicaciones en la consistencia de las teorías de conjuntos y son relevantes en el estudio de la hipótesis del continuo.
Propiedades y Resultados
El estudio de los grandes cardinales permite la formulación de varias propiedades que trascienden la teoría de conjuntos estándar. Uno de los resultados más destacados es el hecho de que los grandes cardinales son consistentes con los axiomas de Zermelo-Fraenkel (ZF), más allá de la teoría estándar de los conjuntos. Además, muchos teoremas en la teoría de conjuntos pueden ser formulados en términos de estos cardinales, como el Teorema de la Hipótesis del Continuo, que se ve afectado por la existencia de ciertos grandes cardinales.
Importancia en la Lógica Matemática
Los grandes cardinales son cruciales en la lógica matemática porque permiten extender y formular nuevas teorías sobre la estructura infinita de los conjuntos. Por ejemplo, ayudan a resolver problemas como la hipótesis del continuo y otros relacionados con la topología de los conjuntos de números reales y la estructura de los modelos de teoría de conjuntos.