Combinaciones Simples en Lógica Matemática
Las combinaciones simples son un concepto central en combinatoria y teoría de conjuntos, áreas fundamentales dentro de la lógica matemática. A diferencia de las permutaciones, donde el orden de los elementos sí importa, las combinaciones se refieren a la selección de elementos donde el orden no tiene importancia. Este principio es útil en una amplia variedad de problemas en matemáticas y ciencias aplicadas, como el cálculo de probabilidades, la organización de elementos y la selección de subconjuntos.
Definición y Fórmula de las Combinaciones Simples
Una combinación simple de un conjunto de 
elementos es una selección de 
elementos de ese conjunto sin tener en cuenta el orden en que se elijan. En otras palabras, el orden de los elementos seleccionados no influye en el número de combinaciones posibles.
La fórmula general para calcular el número de combinaciones simples posibles al seleccionar elementos de un conjunto de elementos es:
$$ \Large C(n, k) = \frac{n!}{k!(n-k)!} $$
Donde:
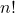es el f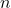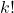actorial de .
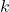es el factorial de .
es el factorial de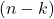 
.
Este número representa cuántas maneras diferentes podemos seleccionar un subconjunto de elementos de un conjunto de elementos, sin que el orden de selección importe.
Propiedades de las Combinaciones Simples
Las combinaciones simples tienen varias propiedades que son fundamentales en la resolución de problemas combinatorios y en el análisis de conjuntos:
- Simetría: La cantidad de combinaciones de 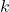elementos de un conjunto de 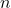elementos es igual a la cantidad de combinaciones de
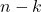elementos del mismo conjunto. Es decir:
$$ \Large C(n, k) = C(n, n-k) $$
Esto refleja la simetría en la elección de elementos: elegir elementos es lo mismo que no elegir los elementos restantes.
Propiedad de la Combinación Total: La suma de las combinaciones de un conjunto de elementos, seleccionando elementos para cada valor de (desde 0 hasta ), es igual al total de los subconjuntos posibles del conjunto. Esto está dado por:
$$ \Large \sum_{k=0}^{n} C(n, k) = 2^n $$
Esto muestra que el número total de subconjuntos posibles de un conjunto de elementos es igual a 
, que es el total de todas las combinaciones posibles, incluyendo el conjunto vacío y el conjunto completo.
Combinaciones con Reemplazo: Si los elementos se pueden repetir en las combinaciones (combinaciones con reemplazo), entonces la fórmula cambia. En este caso, el número de combinaciones con reemplazo de elementos de un conjunto de elementos es:
$$ \Large C'(n, k) = \frac{(n+k-1)!}{k!(n-1)!} $$
Este tipo de combinaciones es útil en situaciones donde los elementos pueden ser seleccionados más de una vez.
Ejemplos de Combinaciones Simples
- Ejemplo 1: Si tenemos un conjunto de 5 elementos
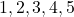y queremos seleccionar 2 elementos, el número de combinaciones posibles es:
$$ \Large C(5, 2) = \frac{5!}{2!(5-2)!} = \frac{5 \times 4}{2 \times 1} = 10 $$
Las combinaciones posibles son: 
.
Ejemplo 2: Si tenemos 4 cartas de una baraja y queremos elegir 3 de ellas, el número de combinaciones posibles es:
$$ \Large C(4, 3) = \frac{4!}{3!(4-3)!} = \frac{4}{1} = 4 $$
Las combinaciones posibles son: 
.
Ejemplo 3: Si tenemos un conjunto de 6 estudiantes y queremos seleccionar 3 para un proyecto, el número de combinaciones posibles es:
$$ \Large C(6, 3) = \frac{6!}{3!(6-3)!} = \frac{6 \times 5 \times 4}{3 \times 2 \times 1} = 20 $$
Aplicaciones de las Combinaciones Simples
Las combinaciones simples tienen una gran variedad de aplicaciones en diferentes campos de las matemáticas y las ciencias. Algunas de las aplicaciones más comunes incluyen:
- Cálculo de probabilidades: En la teoría de probabilidad, las combinaciones se utilizan para calcular la probabilidad de eventos que involucran la selección de elementos sin importar el orden, como en el caso de la selección de cartas en un mazo o la elección de un equipo de trabajo.
- Problemas de selección: Las combinaciones se utilizan cuando se debe elegir un subconjunto de elementos de un conjunto mayor, por ejemplo, elegir un grupo de personas para un comité o seleccionar un subconjunto de objetos de una colección.
- Teoría de grafos: En problemas de teoría de grafos, las combinaciones se emplean para contar el número de formas de seleccionar un conjunto de vértices o aristas de un grafo.
Relación con las Permutaciones
Es importante resaltar la diferencia entre combinaciones y permutaciones. Mientras que las permutaciones tienen en cuenta el orden de los elementos seleccionados, las combinaciones simplemente cuentan el número de formas en que los elementos pueden ser seleccionados sin importar el orden. Por ejemplo, al seleccionar 3 cartas de un mazo, la combinación 
es la misma que 
, mientras que en las permutaciones estas serían consideradas diferentes.
Conclusión
Las combinaciones simples son fundamentales en lógica matemática y combinatoria. Este concepto es clave para resolver problemas que involucran la selección de elementos donde el orden no importa, y tiene aplicaciones en la teoría de probabilidades, la teoría de conjuntos y diversas ramas de las matemáticas aplicadas. Conocer y entender cómo calcular combinaciones es esencial para abordar una amplia gama de problemas en las ciencias matemáticas.