Combinaciones con Repetición en Lógica Matemática

Combinaciones con Repetición en Lógica Matemática

Las combinaciones con repetición son un concepto fundamental en el área de la combinatoria y se utilizan cuando queremos seleccionar elementos de un conjunto donde el orden no importa y se permite la repetición de elementos. Este tipo de combinaciones se emplea en muchos campos de las matemáticas discretas y la teoría de conjuntos, y es esencial para resolver problemas que involucran la selección de elementos cuando las repeticiones son posibles.

Definición de Combinaciones con Repetición

Una combinación con repetición de un conjunto de elementos consiste en seleccionar \( k \) elementos de dicho conjunto, donde los elementos seleccionados pueden repetirse, pero el orden de selección no tiene importancia.

La fórmula para calcular el número de combinaciones con repetición es:

$$ \Large C(n + k – 1, k) = \frac{(n + k – 1)!}{k!(n – 1)!} $$

Donde:

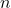• es el número de elementos disponibles para la selección.
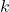• es el número de elementos a seleccionar.

Esta fórmula se deriva del concepto de asignar elementos a categorías diferentes, donde las repeticiones son permitidas.

Propiedades de las Combinaciones con Repetición

Las combinaciones con repetición tienen varias propiedades que las hacen útiles para resolver diferentes problemas matemáticos. Algunas de las principales propiedades incluyen:

1. No importa el orden: A diferencia de las permutaciones, en las combinaciones con repetición el orden de los elementos seleccionados no afecta al resultado. Por ejemplo, seleccionar 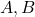es lo mismo que seleccionar .
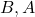2. Permiten repeticiones: A diferencia de las combinaciones sin repetición, las combinaciones con repetición permiten que los elementos se repitan en la selección. Esto es útil cuando, por ejemplo, se deben distribuir elementos idénticos en grupos o asignar recursos con posibilidad de repetición.
3. Relación con las particiones: Las combinaciones con repetición están estrechamente relacionadas con los problemas de particiones, donde se dividen elementos en grupos de tamaño fijo, permitiendo que se repitan elementos.

Ejemplos de Combinaciones con Repetición

1. Ejemplo 1: Si tenemos 3 colores y queremos elegir 2 colores para formar una combinación (sin importar el orden), el número de combinaciones con repetición es:

$$ \Large C(3 + 2 – 1, 2) = C(4, 2) = \frac{4!}{2!2!} = 6 $$

Las combinaciones posibles son: .

Ejemplo 2: Si tenemos 5 tipos de frutas y queremos elegir 3 frutas, permitiendo repeticiones, el número de combinaciones con repetición es:

$$ \Large C(5 + 3 – 1, 3) = C(7, 3) = \frac{7!}{3!4!} = 35 $$

Las combinaciones posibles incluyen secuencias como: .

Ejemplo 3: Si tenemos 4 diferentes colores de bolas y queremos seleccionar 2 bolas (permitiendo repeticiones), el número de combinaciones con repetición es:

$$ \Large C(4 + 2 – 1, 2) = C(5, 2) = \frac{5!}{2!3!} = 10 $$

Las combinaciones posibles incluyen: .

Aplicaciones de las Combinaciones con Repetición

Las combinaciones con repetición tienen muchas aplicaciones prácticas en diversas ramas de las matemáticas y otras ciencias. Algunas aplicaciones clave incluyen:

1. Distribución de Recursos: En problemas donde se deben distribuir recursos entre diferentes grupos o personas, las combinaciones con repetición permiten calcular las diversas formas en las que se puede hacer esta distribución, considerando que se pueden repetir los recursos en algunos grupos.
2. Problemas de Partición: En teoría de particiones, las combinaciones con repetición se utilizan para contar el número de formas de dividir un conjunto de elementos en grupos, permitiendo que algunos elementos aparezcan en múltiples grupos.
3. Cálculo de Códigos: En la teoría de la información, las combinaciones con repetición se utilizan para calcular las diferentes maneras en que se pueden formar secuencias de códigos o palabras cuando se permite la repetición de símbolos.
4. Selección de Subconjuntos en Juegos de Azar: En juegos de azar, como en las loterías o en la distribución de premios, las combinaciones con repetición son útiles para calcular las diferentes combinaciones de números o elementos que pueden ser seleccionados de un conjunto limitado.
5. Algoritmos de Optimización: En algunos algoritmos de optimización y análisis de redes, las combinaciones con repetición se aplican para contar las formas en que se pueden agrupar o organizar elementos de manera eficiente.

Conclusión

Las combinaciones con repetición son un concepto esencial en la combinatoria y la enumeración, y son fundamentales para resolver una amplia variedad de problemas matemáticos en los que el orden no importa y los elementos pueden repetirse. Su comprensión es crucial en diversos campos de la lógica matemática, la teoría de la información, y la optimización de recursos.