Coeficientes Binomiales en Lógica Matemática
Los coeficientes binomiales son una de las herramientas más fundamentales en la combinatoria y la enumeración en el campo de la lógica matemática. Son esenciales para resolver problemas en los que se requieren cálculos sobre la selección y organización de elementos de un conjunto. Este concepto está profundamente relacionado con el binomio de Newton y tiene aplicaciones en diversas ramas de las matemáticas discretas, como la teoría de conjuntos, la teoría de grafos y la probabilidad.
Definición de los Coeficientes Binomiales
El coeficiente binomial, denotado como 
, representa el número de formas en las que se pueden seleccionar 
elementos de un conjunto de 
elementos sin importar el orden de selección. En otras palabras, es el número de combinaciones sin repetición posibles que se pueden formar a partir de un conjunto de elementos.
La fórmula para calcular el coeficiente binomial es:
$$ \Large \binom{n}{k} = \frac{n!}{k!(n – k)!} $$
Donde:
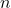- es el número total de elementos del conjunto.
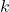- es el número de elementos a seleccionar.
denota el factorial de un número, que es el producto de todos los números enteros positivos hasta ese número. Por ejemplo, 
.
Propiedades de los Coeficientes Binomiales
Los coeficientes binomiales tienen varias propiedades importantes que los hacen útiles para resolver una amplia variedad de problemas combinatorios. Algunas de las propiedades clave incluyen:
- Simetría: Los coeficientes binomiales tienen una propiedad de simetría que establece que:
$$ \Large \binom{n}{k} = \binom{n}{n – k} $$
Esto significa que el número de formas de seleccionar elementos de un conjunto de elementos es igual al número de formas de seleccionar los 
elementos restantes.
Identidad de Pascal: Una de las identidades más importantes de los coeficientes binomiales es la identidad de Pascal, que dice que:
$$ \Large \binom{n}{k} = \binom{n – 1}{k – 1} + \binom{n – 1}{k} $$
Esta relación es útil para calcular los coeficientes binomiales de manera recursiva.
Relación con el binomio de Newton: Los coeficientes binomiales son los coeficientes que aparecen en el desarrollo del binomio de Newton, donde:
$$ \Large (x + y)^n = \sum_{k=0}^{n} \binom{n}{k} x^{n – k} y^k $$
Esta fórmula muestra cómo se expanden las potencias de un binomio, y los coeficientes binomiales indican cuántas formas se pueden elegir los términos de la expansión.
Valor especial: Existen algunos valores especiales para los coeficientes binomiales:
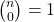para todo 
.
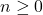para tod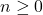o .
cuando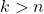 
.
Ejemplos de Coeficientes Binomiales
- Ejemplo 1: Si tenemos un conjunto de 5 elementos
y queremos seleccionar 2 elementos, el número de formas de hacerlo es:
$$ \Large \binom{5}{2} = \frac{5!}{2!(5 – 2)!} = \frac{5 \times 4}{2 \times 1} = 10 $$
Las combinaciones posibles son: 
.
Ejemplo 2: Si tenemos un conjunto de 6 elementos 
y queremos seleccionar 3 elementos, el número de formas de hacerlo es:
$$ \Large \binom{6}{3} = \frac{6!}{3!(6 – 3)!} = \frac{6 \times 5 \times 4}{3 \times 2 \times 1} = 20 $$
Las combinaciones posibles incluyen secuencias como: 
.
Ejemplo 3: Si tenemos 10 elementos 
y queremos seleccionar 4 elementos, el número de combinaciones posibles es:
$$ \Large \binom{10}{4} = \frac{10!}{4!(10 – 4)!} = \frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1} = 210 $$
Las combinaciones posibles son todas las selecciones de 4 elementos de los 10 disponibles.
Aplicaciones de los Coeficientes Binomiales
Los coeficientes binomiales tienen una amplia gama de aplicaciones en combinatoria, teoría de conjuntos, teoría de probabilidades y otras áreas de las matemáticas discretas. Algunas de las aplicaciones más comunes incluyen:
- Conteo de Combinaciones: Los coeficientes binomiales se utilizan para contar el número de maneras en las que se pueden seleccionar subconjuntos de un conjunto dado, lo que es esencial para resolver problemas de combinatoria.
- Probabilidad: En la teoría de probabilidades, los coeficientes binomiales se utilizan en el cálculo de probabilidades en experimentos de Bernoulli, como en el caso de la distribución binomial.
- Cálculo de Expansiones de Binomios: Los coeficientes binomiales son fundamentales para el desarrollo de los binomios en el binomio de Newton, lo cual es crucial en el álgebra.
- Teoría de Grafos: En la teoría de grafos, los coeficientes binomiales se utilizan para contar las formas posibles de conectar nodos en ciertas estructuras de grafos.
Conclusión
Los coeficientes binomiales son un concepto esencial en la combinatoria y en la enumeración dentro de la lógica matemática. Su aplicación en la resolución de problemas combinatorios y su presencia en varias ramas de las matemáticas hacen que su comprensión sea clave para abordar problemas complejos en teoría de conjuntos, álgebra, probabilidad y más.